A couple of days ago, I supplied readers of this (sadly mathematical-leaning) blog a formula for finding the square root of numbers between 3 and 10 approximately. The formula was:
Actually, I can explain the idea fairly easily, starting at a very crude approximation formula indeed, and proceeding to a formula that is a little more tricky, from where it is just a small hop of faith to the one that I gave.
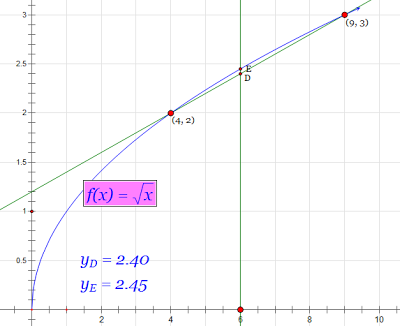
The first step is just to use a line. The square root of 4 is 2, and the square root of 9 is 3. The first fact is represented by (4, 2), where 4 is the number, and 2 is the square root. The second fact is represented by (9, 3). For all numbers between 4 and 9, and a little to the left of 4, and a little to the right of 9, the line joining the two points (4, 2) and (9, 3) serves as an approximation to the square-root curve. If you want to see the line and the curve side-by-side, or rather, superimposed for comparison, here they are:
The rough square root of 6 is, according to this line, 2.4.
The exact square root is, according to the little calculator I have on my PC, 2.449489742783178 (and even that is approximate, as most of you realize, only it's certainly a lot more accurate than 2.4).
Now, how does one go about getting this 2.4 approximate value? Well, as you must have suspected, it is a matter of ratios and proportions, and your Dad could have probably figured it out, even if he had no mathematics training whatsoever, simply by using the sorts of skills they taught people back before calculators. It is called interpolating. You say, well, 6 is 2/5 the way from 4 to 9, so the square root of 6 must be roughly 2/5 the way from 2 to 3, and you get 2 + (2/5)1 = 2.4!!!
Now, in order to proceed, we need to do a tiny bit of algebra. I mean, algebra was invented to further the progress of mathematics, and though I'm trying to minimize the algebra, I can't avoid it completely. All I want to do, (and I'm trying not to sound obnoxiously apologetic) is to write the ratio-and-proportion method above using x's. The formula is
If you put in x = 9, the first (red) fraction becomes zero. The second fraction becomes 1, so that the formula reduces to 3, magic again! So this is a formula that gives the correct y-values at the two points we want.
Next, I have to convince you that this formula represents a line. Algebra specialists can tell that by just inspection: there are no squares, no cubes, no nothing; in fact, just a tiny bit more algebra simplifies the formula to .4(9–x) + .6(x–4), or .2x + 1.2. This one is obviously the equation of a line, and it is the correct line, if you put in x = 4 (which gives you 2), and x=9, which gives you 3. So, if you want a very rough approximation indeed, use this one, for any numbers between 3 and 10.
I know I am very lazy when I'm checking the Web, so I should give you a table of square roots from this formula, and very accurate square roots, so that you can do a number-by number comparison of the exact versus approximate values. (Don't forget that the 'exact' values are only exact up to however many decimal places I'm going to give you, and I think I will give you, er, 5. Just to save space. Here you go:
x
|
√x -approximate
|
√x -"exact"
|
Difference
|
3.0
|
1.8
|
1.73205
|
0.068
|
3.5
|
1.9
|
1.87083
|
0.029
|
4.0
|
2
|
2.00000
|
0.000
|
4.5
|
2.1
|
2.12132
|
-0.021
|
5.0
|
2.2
|
2.23607
|
-0.036
|
5.5
|
2.3
|
2.34521
|
-0.045
|
6.0
|
2.4
|
2.44949
|
-0.049
|
6.5
|
2.5
|
2.54951
|
-0.050
|
7.0
|
2.6
|
2.64575
|
-0.046
|
7.5
|
2.7
|
2.73861
|
-0.039
|
8.0
|
2.8
|
2.82843
|
-0.028
|
8.5
|
2.9
|
2.91548
|
-0.015
|
9.0
|
3
|
3.00000
|
0.000
|
9.5
|
3.1
|
3.08221
|
0.018
|
10.0
|
3.2
|
3.16228
|
0.038
|
Whoa! Can you dig it?
The approximate square roots are clearly increasing in uniform steps, and just as clearly, can't possibly be the exact square roots. But they're certainly correct at two points: 4 and 9, no surprise! But wait:
The exact square roots are horrible numbers (well, not particularly horrible...) and are sometimes slightly larger than the approximate value, and sometimes slightly smaller. Actually, between 4 and 9 they're larger. The exact square-root curve lies above the line, remember?
So, as you can see, we're going to do a lot better with a curve!
Now, let's be serious. Non-math people know very few curves outside circles and parabolas. A circle is just the wrong type of equation, unfortunately, and anyway, the formula of a circle has even worse square roots than a plain ol' square root, let me assure you. A parabola, on the other hand, has the easiest sort of equation next to a line. So next we're going to try a parabolic approximation.
The easiest way to do this is to borrow the exact square root of one of the numbers, ideally the one plumb spang in the middle between 3 and 10: er ... 6.5. Yuck. It's 2.54951, approximately. Wait; let's try 6.25. I'm pretty sure its square root is exactly 2.5 ... Yes, it is. OK, let's use that one.
Here's how we use it. It's little variation on the equation of the line, with red and purple fractions. Each fraction is going to have multiple pairs of parentheses, and there are going to be three fractions. Oh joy, you're probably exclaiming! So here goes.
The formula, please. (Drum roll.)
It is:
You're probably wondering what this formula looks like once it is "simplified". That's what I was afraid of. Arch is getting old, I sweat and strain, body all aching and racked with pain... expand that quadratic, lift that bale, tow that barge,
I got lazy. I got Wolfram Alpha to do it. The result was
-0.00808081 x2 +0.30505051 x + 0.909091
How good is this one? Aha! Now that we have three different approximation formulas, it does get interesting to see which ones are better! The first way is to expand our table, to incorporate the quadratic, or parabolic approximation. This is easy. (For you. For me, there's more towing of barges. But I do it gladly. ... )
x
|
x -"exact"
|
x -linear
|
Diff
|
x-parabolic
|
Diff
|
3.0
|
1.73205
|
1.8
|
0.068
|
1.75152 | 0.019 |
3.5
|
1.87083
|
1.9
|
0.029
|
1.87778 | 0.007 |
4.0
|
2.00000
|
2
|
0.000
|
2 | 0.000 |
4.5
|
2.12132
|
2.1
|
-0.021
|
2.11818 | -0.003 |
5.0
|
2.23607
|
2.2
|
-0.036
|
2.23232 | -0.004 |
5.5
|
2.34521
|
2.3
|
-0.045
|
2.34242 | -0.003 |
6.0
|
2.44949
|
2.4
|
-0.049
|
2.44848 | -0.001 |
6.25
|
2.50000
|
2.45
|
-0.050
|
2.5 | 0.000 |
6.5
|
2.54951
|
2.5
|
-0.050
|
2.55051 | 0.001 |
7.0
|
2.64575
|
2.6
|
-0.046
|
2.64848 | 0.003 |
7.5
|
2.73861
|
2.7
|
-0.039
|
2.74242 | 0.004 |
8.0
|
2.82843
|
2.8
|
-0.028
|
2.83232 | 0.004 |
8.5
|
2.91548
|
2.9
|
-0.015
|
2.91818 | 0.003 |
9.0
|
3.00000
|
3
|
0.000
|
3 | 0.000 |
9.5
|
3.08221
|
3.1
|
0.018
|
3.07778 | -0.004 |
10.0
|
3.16228
|
3.2
|
0.038
|
3.15247 | -0.010 |
Our old linear approximations look a little too simple, in comparison to the parabolic approximations, which go into 5 decimal places. For the most part, you can see that they have at least two decimal places of accuracy, so we could have rounded up the last decimal place. (Giving 5 decimal places when you're only accurate to about 3 is considered misleading, and in terrible taste.)
Look at the new column of differences! They're very small. The worst errors are at the two extremes, 3 and 10. As expected, the error is zero at 4, at 9, and at 6.25!!! How about that!
It only remains to show you all three curves superimposed, so you can see that the parabolic approximation lies closer to the square root than the line.
The parabola is in orange, which is difficult to see. I mean, the orange curve and the blue square root curve are very, very close. However, outside the range between 4 and 9, the two curves diverge dramatically. Here's a larger-scaled picture:
So anyway, the quadratic approximation is very good indeed, but the very first approximation I gave you is better still. After a while, though, the additional accuracy is hardly worth the computational complexity, and using a curve of degree five will probably only gain you a couple more decimal places of accuracy, and give you a lot more work to calculate, when you actually want to get an approximate square root quickly.
Finally, all this mathematics is going to be of theoretical interest only, for the simple reason that when you need a square root, what are the chances it's going to be between 3 and 10, really? But this is the sort of thing math people do, to begin with, to develop tools for studying the business. Similar methods can be used to get any square root approximately, I assure you, but it is too difficult to show you here.
Finally, all this mathematics is going to be of theoretical interest only, for the simple reason that when you need a square root, what are the chances it's going to be between 3 and 10, really? But this is the sort of thing math people do, to begin with, to develop tools for studying the business. Similar methods can be used to get any square root approximately, I assure you, but it is too difficult to show you here.
Arch.
No comments:
Post a Comment